Für jeden dieser Körper zeigen wir die passende Formel zur Volumenberechnung. Wir erklären die Herleitung Schritt für Schritt und rechnen Beispiele durch. Wenn Sie nur Volumeneinheiten wie Liter in Milliliter oder andere Maße umrechnen möchten, nutzen Sie unseren Volumen-Umrechner.
Inhalte zum Thema "Volumen berechnen"
Inhalt
Eingabehilfe zum Volumen-Rechner
Körper
Wählen Sie bitte den geometrischen Körper aus, für den Sie das Volumen berechnen möchten.
Danach blendet der Rechner eine Skizze und die benötigten Maße ein.
Unterstützt werden Quader, Würfel, Zylinder, Kegel, Pyramide und Kugel.
Größeneinheit
Wählen Sie die gewünschte Längeneinheit für Eingaben und Ausgabe: mm, cm, dm, m oder km.
Das Ergebnis wird in der passenden Volumeneinheit (z. B. cm³, m³) ausgegeben.
Eingaben für den ausgewählten Körper
Tragen Sie die geforderten Maße für den gewählten Körper ein (z. B. Kantenlängen, Radius, Höhe). Der Rechner ermittelt daraus automatisch das Volumen.
Skizze
Die Skizze zeigt den ausgewählten geometrischen Körper an.
So können sie sich ein Bild davon machen, wie Quader, Würfel, Zylinder, Kegel, Zylinder Pyramide und Kugel definiert sind.
Die Darstellung passt sich an, sobald Sie einen anderen Körper wählen.
Volumen berechnen für Quader
Zuerst erklären wir kurz, was ein Quader ist. Danach folgt die allgemeine Formel für das Volumen und ein Beispiel, das die Anwendung zeigt.
Definition Quader
Ein Quader ist ein geometrischer Körper mit sechs rechteckigen Seitenflächen. Er besitzt:
- 6 rechteckige Flächen, die paarweise parallel sind und rechtwinklig aufeinander stehen,
- 8 Ecken und
- 12 Kanten (jeweils vier gleich lange, zueinander parallele Kanten).
Formel für das Volumen eines Quaders
Das Volumen V erhält man, indem man Länge, Breite und Höhe miteinander multipliziert.
V = a × b × c
Dabei stehen a, b und c für die drei Kantenlängen (z. B. Länge, Breite, Höhe bzw. Höhe, Breite, Tiefe).
Beispiel: Volumen eines Quaders berechnen
Gegeben: a = 3 cm (Höhe), b = 4 cm (Breite), c = 5 cm (Tiefe). Gesucht: das Volumen V.
Rechnung
Mit V = a × b × c ergibt sich:
V = 3 cm × 4 cm × 5 cm = 60 cm³.
Volumen berechnen für Würfel
Der Würfel ist ein Spezialfall des Quaders. Zunächst folgt eine kurze Definition, dann die Volumenformel und schließlich ein Beispiel zur Berechnung.
Definition Würfel
Ein Würfel ist ein Quader, bei dem alle Kanten gleich lang und alle sechs Flächen Quadrate sind.
Formel für das Volumen eines Würfels
Das Volumen V eines Würfels berechnet sich aus der Kantenlänge a. Da alle drei Dimensionen gleich groß sind, wird a mit sich selbst dreimal multipliziert:
V = a³
Beispiel: Volumen eines Würfels berechnen
Gegeben: a = 3 cm. Gesucht: das Volumen V.
Rechnung
Mit der Formel V = a³ ergibt sich:
V = (3 cm)³ = 27 cm³.
Volumen berechnen für Zylinder
Nun geht es um die Berechnung des Volumens für den Zylinder. Nach der Definition folgt die allgemeine Volumenformel, anschließend ein Beispiel zur Anwendung.
Hinweis: Spezieller Zylinder-Rechner
Umfangreichere Berechnungen zum Zylinder – etwa für Volumen, Grundfläche, Mantelfläche und Oberfläche – finden Sie auf unserer Seite zum Zylinder-Rechner.
Definition Zylinder
Ein Zylinder (Kreiszylinder) ist ein geometrischer Körper mit zwei parallelen, gleich großen Kreisflächen, die durch eine Mantelfläche verbunden sind.
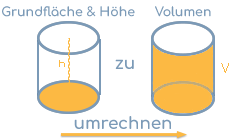
Formel für das Volumen eines Zylinders
Das Volumen V eines Zylinders berechnet sich, indem man den Flächeninhalt der Grundfläche G mit der Höhe h multipliziert:
V = G × h
Beispiel: Volumen eines Zylinders berechnen
Gegeben: Grundfläche G = 3 cm², Höhe h = 5 cm. Gesucht: das Volumen V.
Rechnung
Mit der Formel V = G × h ergibt sich:
V = 3 cm² × 5 cm = 15 cm³.
Weitere Beispiele
Auf folgender Seite mit Beispielen für Zylinder finden Sie weitere Beispiele, z.B. die Berechnung des Volumens aus Radius und Höhe oder über die Mantelfläche.
Volumen berechnen für Kegel
Im Folgenden zeigen wir die Volumenberechnung für den Kegel. Nach der Definition folgt die allgemeine Formel und anschließend mehrere Rechenbeispiele.
Definition Kegel
Ein (gerader) Kreiskegel ist ein geometrischer Körper, der entsteht, wenn alle Punkte einer Kreislinie geradlinig mit einem Punkt außerhalb der Kreisscheibe (der Spitze) verbunden werden.
Die Kreisscheibe ist die Grundfläche, die Kreislinie die Leitkurve (Kante), die Seitenfläche heißt Mantelfläche. Der Abstand vom Mittelpunkt der Grundfläche zur Spitze ist die Höhe h. Steht diese Achse senkrecht auf der Grundfläche, liegt ein gerader Kreiskegel vor.
Formel für das Volumen eines Kegels
Das Volumen V eines Kegels ist ein Drittel aus Grundfläche G mal Höhe h:
V = ⅓ × G × h
Aus Grundfläche und Höhe das Volumen berechnen
Gegeben: G = 3 cm², h = 5 cm. Gesucht: V.
Berechnung
V = ⅓ × G × h = ⅓ × 3 cm² × 5 cm = 5 cm³.
Aus Radius und Höhe das Volumen berechnen
Gegeben: r = 3 cm, h = 5 cm. Gesucht: V.
Berechnung
Mit G = π r² wird aus V = ⅓ × G × h die Formel V = ⅓ × π r² × h.
Einsetzen: V = ⅓ × π × (3 cm)² × 5 cm ≈ 47,12 cm³.
Aus Durchmesser und Höhe das Volumen berechnen
Gegeben: d = 3 cm, h = 5 cm. Gesucht: V.
Berechnung
Mit r = d/2 gilt V = ⅓ × π (d/2)² × h.
Einsetzen: V = ⅓ × π × (3 cm/2)² × 5 cm ≈ 11,78 cm³.
Aus Umfang und Höhe das Volumen berechnen
Gegeben: Umfang U = 3 cm, h = 5 cm. Gesucht: V.
Berechnung
Mit U = 2πr folgt r = U/(2π) und damit V = ⅓ × π × (U/(2π))² × h = ⅓ × U² / (4π) × h
Einsetzen: V = ⅓ × (3 cm)² / (4π) × 5 cm ≈ 1,19 cm³.
Volumen berechnen für Pyramiden
Nun zeigen wir die Volumenberechnung bei Pyramiden. Nach einer kurzen Definition folgt die allgemeine Volumenformel. Anschließend veranschaulichen Beispiele die Rechnung.
Definition Pyramide
Eine (gerade) quadratische Pyramide ist ein geometrischer Körper mit quadratischer Grundfläche und einer Spitze S, die senkrecht über dem Mittelpunkt des Quadrats liegt und mit dessen vier Ecken verbunden ist.
Die Pyramide besitzt fünf Flächen: die quadratische Grundfläche und vier kongruente Dreiecke mit der gemeinsamen Spitze S. Sie ähnelt dem Kegel: Dort ist die Grundfläche rund, hier ist sie eckig. Der Abstand vom Mittelpunkt der Grundfläche zur Spitze ist die Höhe h.
Formel für das Volumen einer Pyramide
Das Volumen V einer Pyramide ist ein Drittel aus Grundfläche G mal Höhe h:
V = ⅓ × G × h
Aus Grundfläche und Höhe das Volumen berechnen
Gegeben: G = 3 cm², h = 5 cm. Gesucht: V.
Berechnung
V = ⅓ × G × h = ⅓ × 3 cm² × 5 cm = 5 cm³.
Aus Grundseite und Höhe das Volumen berechnen
Gegeben: a = 3 cm, h = 5 cm. Gesucht: V.
Berechnung
Für eine quadratische Grundfläche gilt G = a². Damit wird aus V = ⅓ × G × h die Formel V = ⅓ × a² × h.
Einsetzen: V = ⅓ × (3 cm)² × 5 cm = 15 cm³.
Volumen berechnen für Kugeln
Abschließend zeigen wir die Volumenberechnung für die Kugel. Nach der Definition folgt die allgemeine Formel sowie Beispiele mit Radius, Durchmesser, Umfang und Oberfläche.
Definition Kugel
Eine Kugel ist die Menge aller Punkte des Raums, die von einem festen Punkt M (Mittelpunkt) denselben Abstand r haben. Dieser Abstand heißt Radius der Kugel.
Formel für das Volumen einer Kugel
Das Volumen V einer Kugel berechnet sich mit:
V = 4/3 × π × r³
Aus dem Radius das Volumen berechnen
Gegeben: r = 3 cm. Gesucht: V.
Berechnung
V = 4/3 × π × (3 cm)³ ≈ 113,1 cm³.
Aus dem Durchmesser das Volumen berechnen
Gegeben: d = 3 cm. Gesucht: V.
Berechnung
d = 2r ⇒ r = d/2.
Aus V = 4/3 × π × r³ wird V = 4/3 × π × (d/2)³ = 4/3 × π × (1,5 cm)³ ≈ 14,14 cm³.
Aus dem Umfang das Volumen berechnen
Gegeben: U = 3 cm. Gesucht: V.
Berechnung
U = 2πr ⇒ r = U/(2π).
V = 4/3 × π × (U/(2π))³ ≈ 0,46 cm³.
Aus der Oberfläche das Volumen berechnen
Gegeben: O = 3 cm². Gesucht: V.
Berechnung
O = 4πr² ⇒ r = O / (4π).
V = 4/3 × π × (O / (4π))³ ≈ 0,49 cm³.
Weitere Online-Rechner
Volumen umrechnen, Zylinderberechnung, Kreis berechnen, Dreieck-Rechner, Zahlengenerator Zufallszahl, Quadratmeter Rechner, Dreisatzrechner, Brüche berechnen, Datum-Rechner, Zeiteinheiten umrechen, Prozent-Rechner, Taschenrechner
Quellenangaben
Insbesondere die Informationen folgender Quellen haben wir für die Themenwelt "Volumen" verwendet:
Letzte Aktualisierung
Diese Seite der Themenwelt "Volumen" wurde von mir, Michael Mühl, zuletzt am 10.07.2025 redaktionell überprüft oder ergänzt. Sie entspricht dem aktuellen Stand.
Änderungen in Themenwelt "Volumen"
- Veröffentlichung des Bereichs Volumen berechnen nebst dazugehöriger Texte.
- Redaktionelle Überarbeitung dieser Seite