Alles zum Thema Zylinder: Hier finden Sie einfache Erklärungen, Formeln und Berechnungen für Volumen, Mantelfläche, Oberfläche, Höhe, Radius, Durchmesser und Umfang. Mithilfe des Rechners können Sie alle diese Werte ganz bequem berechnen.
Das Wichtigste in Kürze
- Hier finden Sie alle wichtigen Definitionen und Formeln zur Berechnung eines Zylinders.
- Sie erfahren Schritt für Schritt, wie man Durchmesser, Volumen, Grundfläche, Höhe und Mantelfläche berechnet.
- Oder Sie nutzen einfach unseren Zylinder-Rechner oben auf der Seite.
Folgende Seiten empfehle ich
Inhalte zum Thema Zylinder
Inhalt
So funktioniert der Zylinder-Rechner
Mit dem Zylinder-Rechner können Sie die wichtigsten geometrischen Größen eines Zylinders – wie Volumen, Grundfläche, Mantelfläche und Oberfläche – einfach und schnell berechnen.
Geben Sie dazu zwei bekannte Werte ein, zum Beispiel Durchmesser und Höhe, und wählen Sie die gewünschte Maßeinheit aus. Der Rechner ermittelt automatisch alle weiteren Zylindermaße und zeigt sie übersichtlich an.
In der angezeigten Skizze werden die gewählten Größen zur besseren Orientierung dargestellt. So sehen Sie direkt, welche Maße eingegeben wurden und wie sie im Zylinder zueinander stehen.
Das Ergebnis enthält sowohl das Volumen in Kubikeinheiten als auch die Mantel- und Oberflächenwerte in Quadrateinheiten. Auf diese Weise können Sie das Fassungsvermögen oder die benötigte Materialfläche eines Zylinders schnell und präzise berechnen.
Der Zylinder-Rechner eignet sich für Berechnungen im Alltag, in Schule und Studium oder auch in der Technik, wenn es um Behälter, Rohre oder andere zylindrische Formen geht.
Eingabehilfe zum Zylinder-Rechner zur Berechnung von Volumen, Grundfläche, Höhe, Mantelfläche und mehr
Größeneinheit
Wählen Sie die gewünschte Einheit aus, in der Sie Ihre Werte eingeben und die Ergebnisse anzeigen möchten.
Sie können zwischen mm, cm, dm, m und km wählen.
Erste Zylindereigenschaft wählen: Radius, Durchmesser, Umfang oder Grundfläche
Wählen Sie eine der vier Eigenschaften – Radius, Durchmesser, Umfang oder Flächeninhalt – und geben Sie den entsprechenden Wert ein.
Bei einem Zylinder werden zuerst die beiden kreisförmigen Grundflächen berechnet. Eine Getränkedose ist ein gutes Beispiel: Boden und Deckel bilden diese Grundflächen. Für die Berechnung reicht es aus, wenn eine der vier genannten Eigenschaften bekannt ist.
Zweite Zylindereigenschaft wählen: Höhe, Volumen oder Mantelfläche
Wählen Sie nun eine der drei weiteren Eigenschaften – Höhe, Volumen oder Mantelfläche – und tragen Sie den Wert ein.
Neben der Berechnung der Grundfläche ist noch eine dieser Angaben nötig, um alle übrigen Maße des Zylinders zu bestimmen. Sobald eine zweite Eigenschaft bekannt ist, kann der Rechner sämtliche geometrischen Größen des Zylinders berechnen.
Skizze
Die Skizze zeigt die gewählte Kombination der Zylindereigenschaften.
So erkennen Sie leicht, wie Radius, Durchmesser, Umfang, Grundfläche, Höhe, Volumen und Mantelfläche zusammenhängen.
Die Darstellung ändert sich automatisch, sobald Sie eine andere Eigenschaft auswählen.
Definition Zylinder
Ein Zylinder (auch Kreiszylinder genannt) ist ein geometrischer Körper.
Er besteht aus zwei gleich großen, parallelen Kreisflächen, die durch eine Mantelfläche miteinander verbunden sind.
Typische Beispiele für Zylinderformen sind eine Getränkedose, ein Getreidesilo oder ein Trinkglas.
Wichtige Eigenschaften eines Zylinders sind der Radius, der Durchmesser, der Umfang, die Grundfläche, die Höhe, das Volumen, die Mantelfläche und die Oberfläche. Mithilfe des Zylinder-Rechners können Sie alle diese Werte einfach berechnen oder umrechnen. Im Anschluss finden Sie weitere Erklärungen und Formeln zur Zylinderberechnung.
Radius eines Zylinders
Der Radius der kreisförmigen Grundfläche eines Zylinders ist der Abstand vom Mittelpunkt bis zum äußeren Rand dieser Fläche. Der Zylinderradius beschreibt also den Abstand von der Mittelachse des Zylinders bis zur Mantelfläche.
Definition Zylinderradius
Der Zylinderradius (r), auch Halbmesser genannt, ist der Abstand zwischen der Mittelachse des Zylinders – also dem Mittelpunkt der Grundfläche – und dem Mantel (M).
Durchmesser eines Zylinders – Definition und Formel
Definition Zylinderdurchmesser
Der Zylinderdurchmesser (d bzw. ⌀) ist die Länge der Geraden, die zwei gegenüberliegende Punkte des Kreisrandes verbindet und durch den Mittelpunkt M der Grundfläche verläuft.
Der Durchmesser beschreibt also die „Dicke“ oder Breite der kreisförmigen Grundfläche eines Zylinders.
Formel Zylinderdurchmesser
Der Durchmesser (d bzw. ⌀) eines Zylinders ist genau doppelt so groß wie sein Radius (r):
d = 2 × r
Umfang eines Zylinders – Definition und Formel
Definition Zylinderumfang
Der Umfang (U) eines Zylinders ist die Länge der Kreislinie, also der Rand der kreisförmigen Grundfläche.
Formel Zylinderumfang
Der Umfang des Zylinders wird berechnet, indem der Durchmesser (d) mit der Kreiszahl Pi (π ≈ 3,1415) multipliziert wird:
U = d × π
Grundfläche eines Zylinders – Definition und Formel
Definition Zylindergrundfläche
Die Grundfläche (G) eines Zylinders ist die kreisförmige Fläche am Boden oder an der Oberseite des Zylinders. Sie wird durch den Mantel des Zylinders begrenzt.
Formel Zylindergrundfläche
Die Grundfläche (G) wird berechnet, indem der Radius (r) mit sich selbst multipliziert und das Ergebnis mit der Kreiszahl Pi (π ≈ 3,1415) multipliziert wird:
G = r² × π
Höhe eines Zylinders – Definition und Formel
Die Höhe (h) eines Zylinders ist der Abstand zwischen seinen beiden Grundflächen, die parallel zueinander liegen. Am Beispiel einer Getränkedose entspricht die Zylinderhöhe einfach der Höhe der Dose.
Definition Zylinderhöhe
Die Zylinderhöhe (h) ist der senkrechte Abstand zwischen den beiden parallelen Grundflächen des Zylinders.
Volumen eines Zylinders – Definition und Formel
Definition Zylindervolumen
Das Volumen (V) eines Zylinders beschreibt, wie viel Raum der Zylinder einnimmt – also den gesamten Inhalt zwischen seinen beiden Grundflächen.
Formel Zylindervolumen
Das Volumen (V) eines Zylinders berechnet sich, indem man den Inhalt der Grundfläche (G) mit der Höhe (h) multipliziert:
V = G × h
Da die Grundfläche eines Zylinders ein Kreis ist, kann die Formel auch mit dem Radius (r) geschrieben werden:
V = π × r² × h
Mantelfläche eines Zylinders – Definition und Formel
Definition Zylindermantelfläche
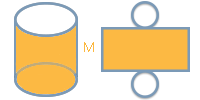
Die Mantelfläche (M) eines Zylinders entsteht, wenn man den Zylindermantel „abwickelt“. Es ergibt sich ein Rechteck, dessen Länge dem Umfang (U) und dessen Breite der Höhe (h) des Zylinders entspricht.
Formel Zylindermantelfläche
Die Mantelfläche (M) wird berechnet, indem man die Zylinderhöhe (h) mit dem Umfang (U) multipliziert:
M = h × U
Da der Umfang U = 2 × π × r ist, kann die Formel auch direkt mit dem Radius (r) geschrieben werden:
M = 2 × π × r × h
Oberfläche eines Zylinders – Definition und Formel
Definition Zylinderoberfläche
Die Oberfläche (O) eines Zylinders besteht aus der Mantelfläche (M) und den beiden kreisförmigen Grundflächen. Sie setzt sich also aus der doppelten Grundfläche (2 × G) und der Mantelfläche zusammen.
Formel Zylinderoberfläche
Die Oberfläche (O) eines Zylinders berechnet sich, indem man den doppelten Grundflächeninhalt (2 × G) zur Mantelfläche (M) addiert:
O = 2 × G + M
Da G = π × r² und M = 2 × π × r × h, lässt sich die Formel auch direkt mit Radius (r) und Höhe (h) darstellen:
O = 2 × π × r × (r + h)
Dies könnte Sie auch interessieren
Weitere Online-Rechner
Kubikmeter berechnen, Umfang berechnen, Dreieck Rechner, Volumenberechnung, Notenpunkte, Maßstab umrechnen, Flächeneinheiten umrechen, Quadratmeter Rechner, Zufallszahlengenerator, Dreisatz Formel, Bruchrechner, Datum-Rechner, Zeiteinheiten umrechen, Prozent-Rechner, Taschenrechner, Längeneinheiten umrechen, Notenschlüsselrechner, Notenschlüsselrechner mit Knick, Abi-Notenschlüsselrechner
Quellenangaben
Insbesondere die Informationen folgender Quellen haben wir für die Themenwelt "Zylinder" verwendet:
Letzte Aktualisierung
Diese Seite der Themenwelt "Zylinder" wurde von mir, Michael Mühl, zuletzt am 10.07.2025 redaktionell überprüft oder ergänzt. Sie entspricht dem aktuellen Stand.
Änderungen in Themenwelt "Zylinder"
- Veröffentlichung des Bereichs Zylinder Volumen berechnen nebst dazugehöriger Texte.
- Redaktionelle Überarbeitung dieser Seite