Mit dem Dreieck-Rechner können Sie viele Dinge rund um ein Dreieck berechnen – zum Beispiel Fläche, Seiten, Umfang, Winkel und Höhen. Die nötigen Formeln werden im Hilfetext einfach erklärt.
Folgende Seiten empfehle ich
Das Wichtigste in Kürze
Sonderseiten
So funktioniert der Dreieck-Rechner
Mit unserem Dreieck-Rechner können Sie ein Dreieck berechnen. Wählen Sie dazu unter „Welche Werte sind gegeben?“ aus, welche Informationen Sie schon haben – zum Beispiel Seitenlängen oder Winkel. Danach können Sie diese Werte in die passenden Felder eingeben.
Der Rechner ermittelt dann alle weiteren Eigenschaften des Dreiecks und zeigt auch eine Abbildung davon an.
Was andere Leser auch gelesen haben
Eingabehilfe zum Dreieck-Rechner
Welche Werte sind gegeben?
 Bitte wählen Sie aus, welche Werte Sie bereits kennen – zum Beispiel Seiten, Höhen oder Winkel. Damit können Fläche und andere
Eigenschaften des Dreiecks berechnet werden.
Bitte wählen Sie aus, welche Werte Sie bereits kennen – zum Beispiel Seiten, Höhen oder Winkel. Damit können Fläche und andere
Eigenschaften des Dreiecks berechnet werden.
Wenn Sie nur eine Seite und die zugehörige Höhe angeben, kann immerhin die Fläche berechnet werden. Es reicht aber nicht, um das ganze Dreieck genau zu bestimmen.
Um ein Dreieck eindeutig zu berechnen, braucht man mehr Informationen. In den Auswahlmöglichkeiten sehen Sie verschiedene Kombinationen, mit denen ein Dreieck eindeutig bestimmt werden kann. Die Abkürzungen helfen dabei: S steht für eine Seite, W für einen Winkel. Im nächsten Schritt werden alle Auswahlmöglichkeiten genau erklärt.
Eine Seite und dazugehörige Höhe h

Wählen Sie diese Option, wenn Sie eine Seitenlänge (a, b oder c) und die dazugehörige Höhe kennen. Die Höhe ist dabei der Abstand vom gegenüberliegenden Eckpunkt senkrecht zur Seite g (oder ihrer Verlängerung).
Mit einer Seite und der zugehörigen Höhe können Sie die Fläche des Dreiecks berechnen. Andere Werte – wie die restlichen Seiten, Höhen oder Winkel – lassen sich damit aber nicht berechnen.
Alle drei Seiten a, b und c (SSS)
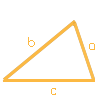
Wählen Sie diese Option, wenn Sie die Längen aller drei Seiten kennen. Diese Kombination nennt man auch „SSS“ (Seite-Seite-Seite).
Damit lässt sich das gesamte Dreieck berechnen: Fläche, Umfang, Höhen zu a, b und c sowie die Winkel α, β und γ.
Eine Seite bei gleichseitigem Dreieck (SSS)

Wählen Sie diese Option, wenn das Dreieck gleichseitig ist – also alle drei Seiten gleich lang sind. Wenn Sie eine Seite kennen, sind automatisch auch die anderen Seiten bekannt.
Diese Variante ist ein Sonderfall der „SSS“-Berechnung, lässt sich aber mit einfacheren Formeln berechnen. Mit nur einer Seitenlänge können Sie die Fläche und alle anderen Eigenschaften des Dreiecks bestimmen.
Zwei Seiten mit eingeschlossenem Winkel (SWS)

Wählen Sie diese Option, wenn Sie zwei Seiten und den dazwischenliegenden Winkel kennen. Diese Kombination nennt man „SWS“.
Damit können Sie die dritte Seite und alle weiteren Eigenschaften des Dreiecks berechnen.
Zwei Katheten bei rechtwinkligem Dreieck (SWS)

Wählen Sie diese Option, wenn Sie ein rechtwinkliges Dreieck haben und die beiden Katheten (die Seiten am rechten Winkel) kennen.
Da der eingeschlossene Winkel 90 Grad beträgt, ist dies ein Spezialfall von „SWS“. Mit den beiden Katheten können Sie alle Eigenschaften des Dreiecks berechnen – auch die Hypotenuse, Fläche, Winkel usw.
Eine Seite und zwei Winkel (SWW, WWS, WSW)

Wählen Sie diese Option, wenn Sie eine Seite und zwei Winkel kennen. Diese Kombination wird oft mit „SWW“, „WWS“ oder „WSW“ abgekürzt.
Mit dem Winkelsummensatz kann der dritte Winkel berechnet werden. Danach können alle anderen Eigenschaften des Dreiecks bestimmt werden.
Zwei Seiten und ein Winkel der längeren Seite gegenüber (SsW, WsS)

Wählen Sie diese Option, wenn Sie zwei Seiten und den Winkel gegenüber der längeren Seite kennen. Diese Fälle werden mit „SsW“ oder „WsS“ abgekürzt.
Damit lässt sich mit dem Sinussatz der Winkel gegenüber der kürzeren Seite berechnen. Anschließend können Sie auch den dritten Winkel und das komplette Dreieck berechnen.
Achtung: Wenn der gegebene Winkel gegenüber der kürzeren Seite liegt, reicht das nicht, um das Dreieck eindeutig zu berechnen.
Dies könnte Sie auch interessieren
Fragen & Tipps zur Dreieck-Berechnung
Hier finden Sie Fragen und hilfreiche Tipps zur Berechnung von Dreiecken. Was ist für Sie besonders relevant?
01.
Was ist ein Dreieck und wie wird es definiert?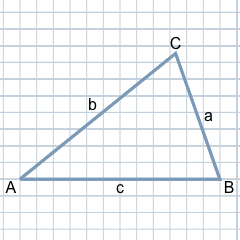
Ein Dreieck entsteht durch drei Punkte in der Ebene, die nicht auf einer Geraden liegen.
Grundlegende Eigenschaften
Die drei Punkte bilden die Ecken des Dreiecks, deren Verbindungslinien die Seiten darstellen. Gemeinsam begrenzen sie eine Fläche in der Ebene. Wir beobachten häufig, dass Anwender besonders an folgenden Eigenschaften interessiert sind:
- Flächeninhalt des Dreiecks
- Länge der drei Seiten
- Gesamtumfang
- Winkel zwischen den Seiten
- Höhen zu den jeweiligen Seiten
Mit unserem Dreieck-Rechner können Sie all diese Werte bequem berechnen und untereinander umrechnen. In der Praxis hat sich gezeigt, dass besonders die Umrechnung zwischen verschiedenen Ausgangswerten für viele Nutzer eine große Arbeitserleichterung darstellt.
02.
Wie wird ein Dreieck korrekt beschriftet?Die Beschriftung der Ecken
Bei einem Dreieck werden die drei Ecken standardmäßig mit den Großbuchstaben A, B und C gekennzeichnet. Wir empfehlen, die Beschriftung gegen den Uhrzeigersinn vorzunehmen, beginnend mit A an der linken unteren Ecke.
Die Benennung der Seiten
Die drei Seiten eines Dreiecks kennzeichnet man mit den Kleinbuchstaben a, b und c. Dabei gilt die Regel: Die Seite a liegt der Ecke A gegenüber, Seite b gegenüber von Ecke B und Seite c gegenüber von Ecke C.
Die Winkelbezeichnungen
Für die drei inneren Winkel des Dreiecks verwendet man die griechischen Buchstaben α (alpha), β (beta) und γ (gamma). Jeder Winkel befindet sich an der entsprechenden Ecke: α bei A, β bei B und γ bei C. In der Praxis zeigt sich, dass diese einheitliche Notation das Verständnis geometrischer Zusammenhänge deutlich erleichtert.
Die Höhenlinien
Die Höhe zu einer Grundseite ist die Lotstrecke vom gegenüberliegenden Eckpunkt zur Grundseite. Wir bezeichnen sie mit ha, hb und hc, wobei der Index angibt, zu welcher Seite die Höhe gemessen wird. Unserer Erfahrung nach ist das korrekte Verständnis der Höhen besonders wichtig für Flächenberechnungen mit dem Dreieck-Rechner.
03.
Welche Arten von Dreiecken gibt es?Einteilung nach Seitenlängen
Je nach Verhältnis der Seitenlängen unterscheiden wir verschiedene Dreieckstypen. In unserer täglichen Arbeit mit dem Dreieck-Rechner begegnen uns am häufigsten diese drei Grundformen:
- Gleichseitiges Dreieck: Alle drei Seiten sind gleich lang (a = b = c). Folglich sind auch alle Winkel gleich groß (60°).
- Gleichschenkliges Dreieck: Zwei Seiten haben die gleiche Länge. Die zugehörigen Winkel sind ebenfalls gleich.
- Ungleichseitiges Dreieck: Alle drei Seiten haben unterschiedliche Längen.
Einteilung nach Winkeln
Nach den Winkelgrößen unterscheiden wir folgende Dreiecksarten:
- Rechtwinkliges Dreieck: Hat einen rechten Winkel (90°). Wir sehen häufig, dass dieser Dreieckstyp besonders oft mit unserem Rechner analysiert wird.
- Spitzwinkliges Dreieck: Alle drei Winkel sind kleiner als 90°.
- Stumpfwinkliges Dreieck: Ein Winkel ist größer als 90°.
Aus unserer Erfahrung ist die Kenntnis dieser Klassifizierungen wichtig, da für bestimmte Dreieckstypen vereinfachte Formeln angewendet werden können, was die Berechnungen mit dem Dreieck-Rechner noch effizienter macht.
04.
Welche Formeln und Sätze sind für Dreiecksberechnungen wichtig?Grundlegende Formeln für den Flächeninhalt
In der Praxis haben sich mehrere Formeln zur Berechnung des Flächeninhalts eines Dreiecks bewährt. Mit unserem Dreieck-Rechner können Sie je nach bekannten Werten die passende Formel verwenden:
- Grundseite und Höhe: A = (g · h) / 2
- Zwei Seiten und eingeschlossener Winkel: A = (a · b · sin(γ)) / 2
- Drei Seiten (Heronsche Formel): A = √(s(s-a)(s-b)(s-c)), wobei s = (a+b+c)/2 der halbe Umfang ist
Der Satz des Pythagoras
Für rechtwinklige Dreiecke gilt der Satz des Pythagoras: a² + b² = c², wobei c die Hypotenuse (längste Seite) ist. Wir haben festgestellt, dass dieser Satz bei vielen Anwendungen des Dreieck-Rechners eine zentrale Rolle spielt.
Die Winkelsumme im Dreieck
Ein fundamentaler Satz besagt, dass die Summe der Innenwinkel in jedem Dreieck stets 180° beträgt: α + β + γ = 180°. Unserer Erfahrung nach ist diese Eigenschaft besonders hilfreich, wenn nur zwei Winkel bekannt sind und der dritte berechnet werden soll.
Der Sinussatz und der Kosinussatz
Für komplexere Berechnungen bieten diese beiden Sätze wertvolle Hilfe:
Sinussatz: a/sin(α) = b/sin(β) = c/sin(γ)
Kosinussatz: a² = b² + c² - 2bc·cos(α)
Wir sehen häufig, dass besonders der Kosinussatz als Verallgemeinerung des Satzes von Pythagoras für nicht-rechtwinklige Dreiecke geschätzt wird. Unser Dreieck-Rechner wendet diese Formeln automatisch an, was komplizierte Handberechnungen überflüssig macht.
Weitere Online-Rechner
Umfang berechnen, Zylinderberechnung, Notenpunkt in Note, Zeugnisschnitt Rechner, Maßstab berechnen, Flächeneinheiten umrechen, Quadratmeter Rechner, Zufallszahlengenerator, Volumen Rechner, Bruch-Rechner, Dreisatz Formel, Datumsrechner, Zeiteinheiten umrechen, Prozent-Rechner, Notenrechner, Notenschlüsselrechner mit Knick, Taschenrechner, Längeneinheiten umrechen, Römische Zahlen berechnen
Quellenangaben
Insbesondere die Informationen folgender Quellen haben wir für die Themenwelt "Dreieck" verwendet:
Letzte Aktualisierung
Diese Seite der Themenwelt "Dreieck" wurde von mir, Michael Mühl, zuletzt am 11.02.2025 redaktionell überprüft oder ergänzt. Sie entspricht dem aktuellen Stand.
Änderungen in Themenwelt "Dreieck"
- Veröffentlichung eines Artikels zum Thema Berechnung gleichseitiger Dreiecke.
- Veröffentlichung eines Artikels zum Thema Flächeninhalt von Dreiecken und zu Rechtwinkligen Dreiecken.
- Veröffentlichung des Bereichs Dreieck berechnen nebst dazugehöriger Texte.
- Redaktionelle Überarbeitung dieser Seite



