Ein gleichseitiges Dreieck ist ein besonderes Dreieck: Alle drei Seiten sind gleich lang. In einem Beispiel zeigen wir, wie man mit einer bekannten Seitenlänge die Fläche, den Umfang, die Winkel und die Höhen berechnen kann. Dafür verwenden wir einfache Formeln, die speziell für gleichseitige Dreiecke gelten.
Folgende Seiten empfehle ich
Spezielle Ratgeber
Auf der Seite zum Dreieck-Rechner finden Sie viele Infos – nicht nur zum gleichseitigen, sondern auch zum allgemeinen Dreieck. Besuchen Sie auch unsere Ratgeber zu den Themen:
Inhalte zum Thema "Gleichseitiges Dreieck"
Inhalt
Einführung zur Berechnung gleichseitiger Dreiecke
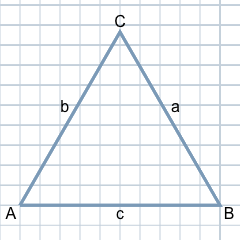 Gleichseitige Dreiecke unterscheiden sich von normalen Dreiecken nur in einem Punkt: Alle drei Seiten sind gleich lang.
Gleichseitige Dreiecke unterscheiden sich von normalen Dreiecken nur in einem Punkt: Alle drei Seiten sind gleich lang.
Ein Dreieck ist genau dann eindeutig bestimmbar, wenn alle drei Seiten bekannt sind. Beim gleichseitigen Dreieck reicht daher eine einzige Seitenlänge, um es vollständig zu berechnen.
Zusätzlich sind die Berechnungen beim gleichseitigen Dreieck einfacher: Alle drei Winkel sind gleich groß – sie betragen immer 60 Grad. Auch die Fläche lässt sich mit einer leichteren Formel berechnen als bei einem normalen Dreieck mit drei verschiedenen Seiten. Das zeigen wir Ihnen im nächsten Schritt.
Beispiel zur Berechnung eines gleichseitigen Dreiecks
Im folgenden Beispiel ist die Seitenlänge a bekannt. Mit diesem einen Wert lassen sich nun alle anderen Eigenschaften des gleichseitigen Dreiecks nach und nach genau berechnen.
Gegeben
Gegeben sei die Seitenlänge a = 5 cm. Da es sich um ein gleichseitiges Dreieck handelt, ist damit auch bereits der Wert aller drei Seiten bekannt.
Gesucht
Gesucht ist die Fläche, der Umfang, die Winkel sowie die Höhen zu allen drei Seiten des gleichseitigen Dreiecks.
Geben Sie die bekannte Seitenlänge a im Rechner für gleichseitige Dreiecke ein. Wählen Sie dafür die Option „Eine Seite bei gleichseitigem Dreieck“ unter „Welche Werte sind gegeben?“ aus.
Der Rechner berechnet dann alle fehlenden Werte und zeigt auch eine grafische Darstellung des Dreiecks an.
Wie wird die Fläche im gleichseitigen Dreieck berechnet?
In einem gleichseitigen Dreieck sind – wie der Name schon sagt – alle drei Seiten gleich lang. Darum kann man die Fläche mit einer einfachen Formel berechnen. Dabei steht a für die Länge einer Seite.
Formel für Fläche im gleichseitigen Dreieck
F = 3 / 4 × a²
Einsetzen des vorhandenen Werts für die Seitenlänge
Setzt man den Wert für a ein, so erhält man
F = 3 / 4 × 5² ≈ 10,83 cm²
Lösung
Die Fläche F des gleichseitigen Dreiecks beträgt 10,83 cm².
Wie wird der Umfang im gleichseitigen Dreieck berechnet?
Wenn die Länge einer Seite bekannt ist, sind beim gleichseitigen Dreieck auch die anderen zwei Seiten gleich lang. Damit lässt sich der Umfang ganz einfach berechnen:
Formel: Umfang U eines gleichseitigen Dreiecks
Der Umfang jedes Dreiecks ist die Summe der Länge aller drei Seiten a, b und c.
U = a + b + c
Einsetzen des vorhandenen Werts
Setzt man den gegebenen Wert a = 5, der ja für jede der drei Seiten gilt ein, so erhält man
U = 5 + 5 + 5 = 15
Lösung
Der Umfang des gleichseitigen Dreiecks beträgt 15 cm.
Wie werden die Winkel im gleichseitigen Dreieck berechnet?
Lösung
In jedem gleichseitigen Dreieck sind alle Winkel gleich groß und betragen jeweils 60°.
Wie werden die Höhen im gleichseitigen Dreieck berechnet?
Zur Berechnung der Höhe zu a im gleichseitigen Dreieck kann anstelle der komplizierteren Formel für allgemeine Dreiecke die folgende Formel genutzt werden
Formel für Höhe zu a im gleichseitigen Dreieck
ha = 3 / 2 × a
Einsetzen der vorhandenen Werte
Setzt man den bekannten Wert für a = 5 cm ein, so erhält man
ha = 3 / 2 × 5 ≈ 4,33
Lösung
Die Höhe zu a, also ha beträgt 4,33 cm.
Weil die Seiten b und c genauso lang sind wie a, sind auch ihre Höhen gleich – also identisch mit der Höhe zu a.
Wie sieht das berechnete gleichseitigen Dreieck aus?
Das gleichseitige Dreieck mit der Seitenlänge a = 5 cm kann mit den berechneten Werten so gezeichnet werden:
Abbildung Ergebnis

1 Kästchen entspricht 0,5 Einheiten (wie im Rechenheft)
Was andere Leser auch gelesen haben
Dies könnte Sie auch interessieren
Weitere Online-Rechner
Umfang berechnen, Zylinderberechnung, Notenpunkt in Note, Zeugnisschnitt Rechner, Maßstab berechnen, Flächeneinheiten umrechen, Quadratmeter Rechner, Zufallszahlengenerator, Volumen Rechner, Bruch-Rechner, Dreisatz Formel, Datumsrechner, Zeiteinheiten umrechen, Prozent-Rechner, Notenrechner, Notenschlüsselrechner mit Knick, Taschenrechner, Längeneinheiten umrechen, Römische Zahlen berechnen
Quellenangaben
Insbesondere die Informationen folgender Quellen haben wir für die Themenwelt "Dreieck" verwendet:
Letzte Aktualisierung
Diese Seite der Themenwelt "Dreieck" wurde von mir, Michael Mühl, zuletzt am 08.07.2025 redaktionell überprüft oder ergänzt. Sie entspricht dem aktuellen Stand.
Änderungen in Themenwelt "Dreieck"
- Veröffentlichung eines Artikels zum Thema Berechnung gleichseitiger Dreiecke.
- Veröffentlichung eines Artikels zum Thema Flächeninhalt von Dreiecken und zu Rechtwinkligen Dreiecken.
- Veröffentlichung des Bereichs Dreieck berechnen nebst dazugehöriger Texte.
- Redaktionelle Überarbeitung dieser Seite



